k-Means clustering
set.seed(90210)
kmodel <- kmeans(scale(hprice2),centers=3,nstart=10)
kmodel$centers
## price crime nox rooms dist radial
## 1 -0.2792677 -0.3600423 -0.07840445 -0.4240612 -0.01224813 -0.5916003
## 2 1.0115090 -0.3971467 -0.77766399 0.9666947 0.75041393 -0.5764852
## 3 -0.6792515 1.0413321 1.00563169 -0.3899504 -0.82541542 1.6253203
## proptax stratio lowstat
## 1 -0.4577160 0.0607907 0.1269073
## 2 -0.6908616 -0.8015948 -0.9236065
## 3 1.5333981 0.8030303 0.8314782
##
## 1 2 3
## 221 151 134
hprice2[,lapply(.SD,mean),by=kmodel$cluster]
## kmodel price crime nox rooms dist radial
## 1: 2 31826.35 0.1999470 4.648940 6.963245 5.376225 4.529801
## 2: 1 19939.77 0.5186833 5.458959 5.986109 3.769955 4.398190
## 3: 3 16256.38 12.5568358 6.714701 6.010075 2.057313 23.701493
## proptax stratio lowstat
## 1: 29.18013 16.72318 6.016358
## 2: 33.10950 18.59095 13.620045
## 3: 66.66716 20.19851 18.719776
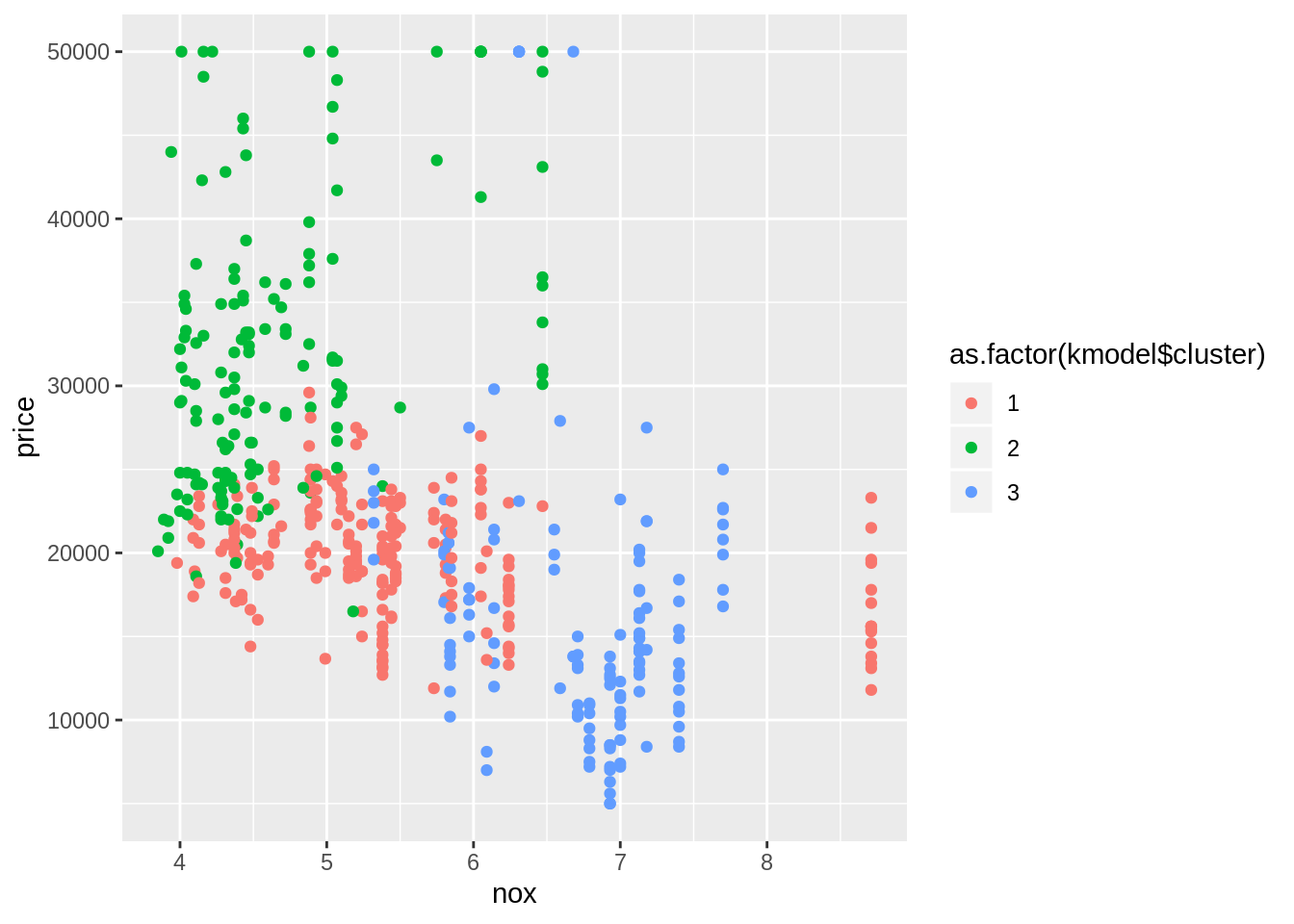
ggplot(hprice2,aes(x=nox,y=price,color=as.factor(kmodel$cluster))) + geom_point()
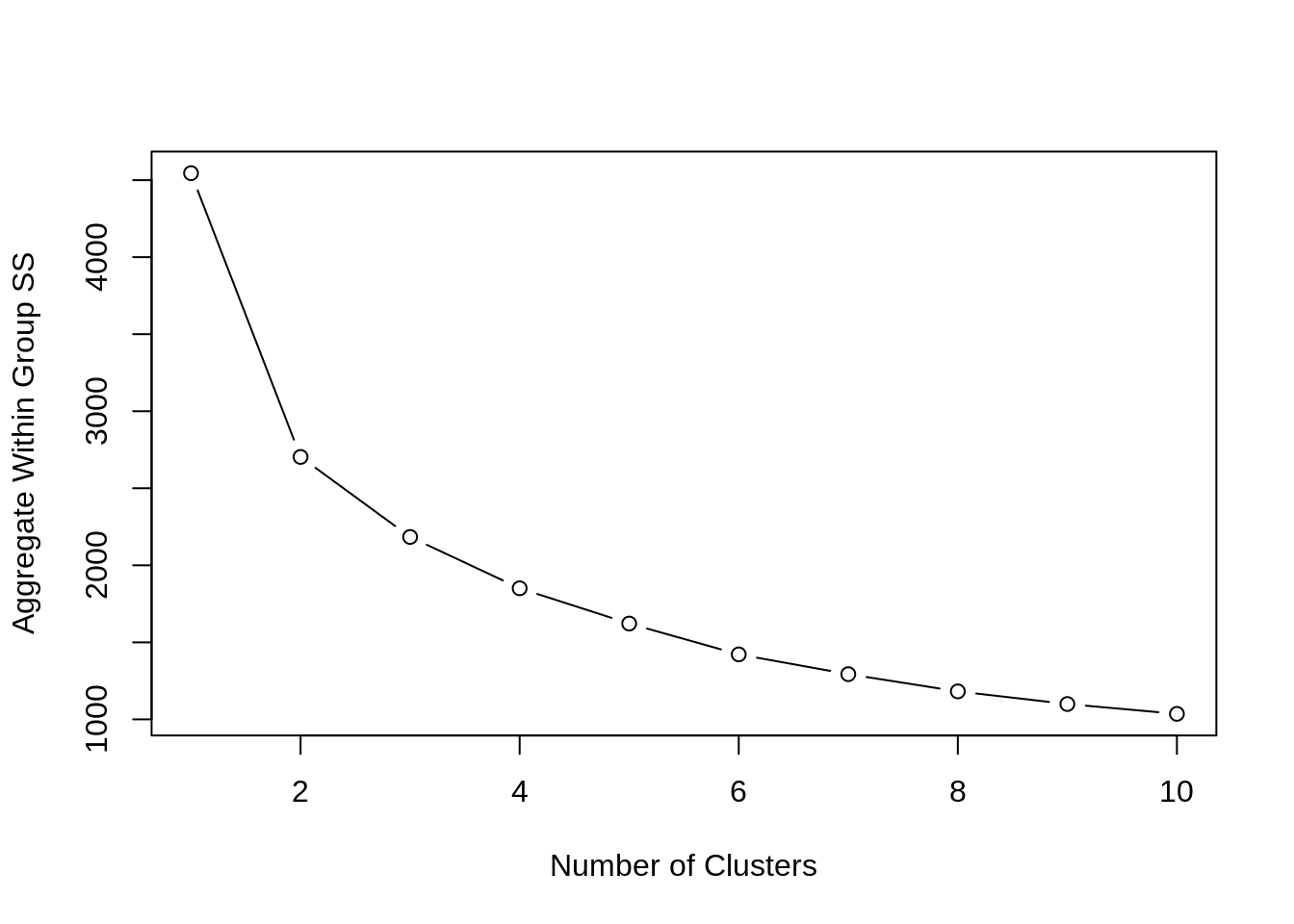
Within group sum of squares
## [1] 2183.669
kmeans.wss(scale(hprice2))
## [1] 4545.000 2703.341 2183.948 1850.740 1621.996 1421.727 1293.463
## [8] 1181.626 1099.631 1035.744
plot.wss(kmeans.wss(scale(hprice2)))
eratio <- function(wss) { # USE MINUS 1 FOR PCA
# Creates the eigenvalue ratio estimator for the number of clusters
n <- NROW(wss)
dss <- -diff(wss) # Create differences in wss (eigenvalues)
dss <- c(wss[1]/log(n),dss) # Assign a zero case
erat <- dss[1:(n-1)]/dss[2:n] # Build the eigenvalue ratio statistic
gss <- log(1+dss/wss) # Create growth rates
grat <- gss[1:(n-1)]/gss[2:n] # Calucluate the growth rate statistic
return(c(which.max(erat),which.max(grat))) # Find the maximum number for each estimator
}
eratio(kmeans.wss(scale(hprice2)))
## [1] 2 2
Hierarchical clustering algorithm
# Model dendrogram
model <- hclust(dist(scale(hprice2)))
summary(cutree(model,k=2))
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 1.000 1.000 1.073 1.000 2.000
hprice2[,lapply(.SD,mean),by=cutree(model,k=3)]
## cutree price crime nox rooms dist radial
## 1: 1 23474.439 1.929987 5.448635 6.349190 3.968465 8.409382
## 2: 2 10503.294 20.348294 6.833824 5.392647 1.611471 24.000000
## 3: 3 8066.667 76.810333 6.810000 6.203333 1.550000 24.000000
## proptax stratio lowstat
## 1: 38.79019 18.32196 11.65881
## 2: 66.60000 20.20000 26.41647
## 3: 66.60000 20.20000 20.27000
plot.wss(hclust.wss(data.table(scale(hprice2))))
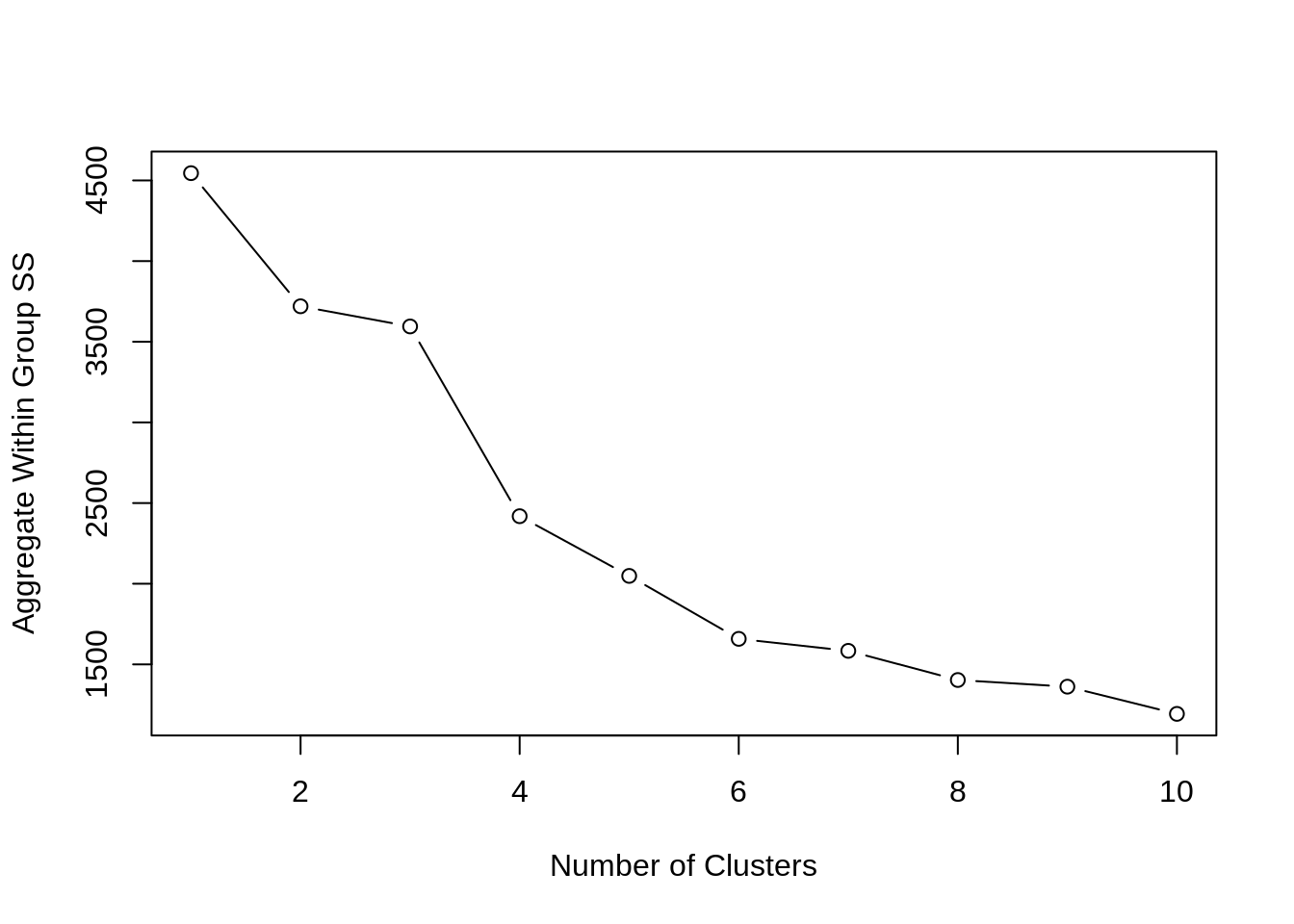
eratio(hclust.wss(data.table(scale(hprice2))))
## [1] 2 2
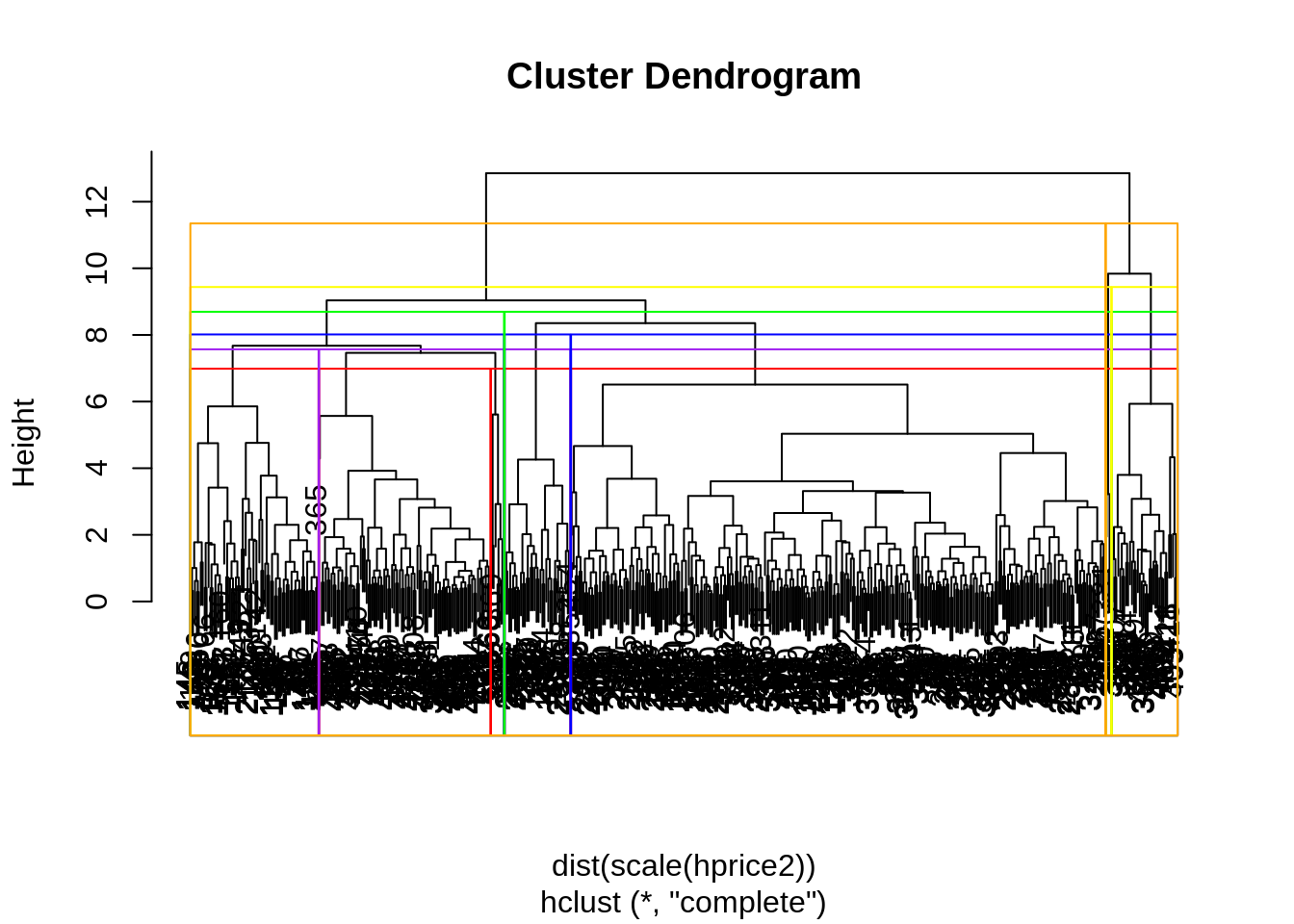
Dendrogram
plot(model)
rect.hclust(model,k=7,border="red")
rect.hclust(model,k=6,border="purple")
rect.hclust(model,k=5,border="blue")
rect.hclust(model,k=4,border="green")
rect.hclust(model,k=3,border="yellow")
rect.hclust(model,k=2,border="orange")
Applying clustering
set.seed(90210)
hprice2$kmean <- kmeans(scale(hprice2),centers=2,nstart=10)$cluster
hprice2$hier <- cutree(hclust(dist(data.table(scale(hprice2)))),k=4)
table(hprice2$hier,hprice2$kmean) # Two-way table to see relationship
##
## 1 2
## 1 235 0
## 2 111 123
## 3 0 34
## 4 0 3
# k-means clustering models
# Pooled:
summary(lm(log(price)~log(nox)+rooms+stratio,data=hprice2))
##
## Call:
## lm(formula = log(price) ~ log(nox) + rooms + stratio, data = hprice2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.02357 -0.13576 0.02406 0.13258 1.40083
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.359458 0.219069 47.288 <2e-16 ***
## log(nox) -0.645329 0.062580 -10.312 <2e-16 ***
## rooms 0.256727 0.018677 13.746 <2e-16 ***
## stratio -0.050873 0.005926 -8.585 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2673 on 502 degrees of freedom
## Multiple R-squared: 0.576, Adjusted R-squared: 0.5734
## F-statistic: 227.3 on 3 and 502 DF, p-value: < 2.2e-16
# Within:
summary(lm(log(price)~as.factor(kmean)+log(nox)+rooms+stratio-1,data=hprice2))
##
## Call:
## lm(formula = log(price) ~ as.factor(kmean) + log(nox) + rooms +
## stratio - 1, data = hprice2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.98976 -0.12245 0.00579 0.11441 1.45933
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## as.factor(kmean)1 9.787719 0.254704 38.428 < 2e-16 ***
## as.factor(kmean)2 9.611210 0.279304 34.411 < 2e-16 ***
## log(nox) -0.357760 0.091938 -3.891 0.000113 ***
## rooms 0.253544 0.018389 13.788 < 2e-16 ***
## stratio -0.042169 0.006185 -6.818 2.67e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2629 on 501 degrees of freedom
## Multiple R-squared: 0.9993, Adjusted R-squared: 0.9993
## F-statistic: 1.448e+05 on 5 and 501 DF, p-value: < 2.2e-16
# hierarchical clustering models
# Pooled:
summary(lm(log(price)~log(nox)+rooms+stratio,data=hprice2))
##
## Call:
## lm(formula = log(price) ~ log(nox) + rooms + stratio, data = hprice2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.02357 -0.13576 0.02406 0.13258 1.40083
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.359458 0.219069 47.288 <2e-16 ***
## log(nox) -0.645329 0.062580 -10.312 <2e-16 ***
## rooms 0.256727 0.018677 13.746 <2e-16 ***
## stratio -0.050873 0.005926 -8.585 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2673 on 502 degrees of freedom
## Multiple R-squared: 0.576, Adjusted R-squared: 0.5734
## F-statistic: 227.3 on 3 and 502 DF, p-value: < 2.2e-16
# Within:
summary(lm(log(price)~as.factor(hier)+log(nox)+rooms+stratio,data=hprice2))
##
## Call:
## lm(formula = log(price) ~ as.factor(hier) + log(nox) + rooms +
## stratio, data = hprice2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.95937 -0.13982 0.01699 0.11803 1.30258
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.10932 0.22968 44.015 < 2e-16 ***
## as.factor(hier)2 -0.06596 0.04174 -1.580 0.115
## as.factor(hier)3 -0.42904 0.06856 -6.258 8.41e-10 ***
## as.factor(hier)4 -0.87087 0.15113 -5.762 1.45e-08 ***
## log(nox) -0.42487 0.08843 -4.805 2.05e-06 ***
## rooms 0.21876 0.01895 11.542 < 2e-16 ***
## stratio -0.04112 0.00634 -6.487 2.11e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2484 on 499 degrees of freedom
## Multiple R-squared: 0.6361, Adjusted R-squared: 0.6317
## F-statistic: 145.4 on 6 and 499 DF, p-value: < 2.2e-16



