4.2 Coding guide
4.2.1 Linear probability model
The data in the mroz table consists of married women in the US in the 1970s. In the data, we are looking at the effect of education, experience, and other personal characteristic on whether or not these women were in the labor force (i.e., either working or unemployed and looking for work). Here the dependent variable is a dummy variable. We have seen cases before where the independent variables are dummies, but here the dependent variable is a dummy. In this case, we say that we have a limited dependent variable.
Running the linear probability model is straightforward:
model1 <- lm(inlf~educ+exper+I(exper^2)+age+kidslt6+kidsge6,data=mroz)
summary(model1)##
## Call:
## lm(formula = inlf ~ educ + exper + I(exper^2) + age + kidslt6 +
## kidsge6, data = mroz)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.93849 -0.38373 0.08641 0.34327 0.93279
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.6219835 0.1538604 4.043 5.84e-05 ***
## educ 0.0325008 0.0070171 4.632 4.28e-06 ***
## exper 0.0404705 0.0056745 7.132 2.34e-12 ***
## I(exper^2) -0.0005890 0.0001853 -3.178 0.00154 **
## age -0.0171779 0.0024487 -7.015 5.16e-12 ***
## kidslt6 -0.2654798 0.0335708 -7.908 9.42e-15 ***
## kidsge6 0.0114753 0.0132197 0.868 0.38565
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4284 on 746 degrees of freedom
## Multiple R-squared: 0.2588, Adjusted R-squared: 0.2528
## F-statistic: 43.4 on 6 and 746 DF, p-value: < 2.2e-16Here we can see a 1 year increase in experience is related to a 3.3% increase in the probability of being in the labor force. We can also see that having a child less than 6 years old is related to a 26% decrease in the probability of being in the labor force. As mentioned in the theoretical portion, it is possible to estimate the probability of being in the labor force as being less than 0 or greater than 1 in some cases. Consider predictions for 3 new women:
newwomen <- data.table(educ=c(16,20,11),exper=c(5,15,3),age=c(30,40,30),kidslt6=c(0,0,3),kidsge6=c(0,2,0))
head(newwomen)## educ exper age kidslt6 kidsge6
## 1: 16 5 30 0 0
## 2: 20 15 40 0 2
## 3: 11 3 30 3 0predict(model1,newwomen)## 1 2 3
## 0.8142860 1.0823650 -0.2161745This is not ideal and is the reason that using logistic regression is prefered.
4.2.2 Logistic regression
To run a logistic (logit) regression, we are going to use a GLM model with the family set to binomial. Here R is going to use the default linking function which is the logit function:
model2 <- glm(inlf~educ+exper+I(exper^2)+age+kidslt6+kidsge6,family=binomial,data=mroz)
summary(model2)##
## Call:
## glm(formula = inlf ~ educ + exper + I(exper^2) + age + kidslt6 +
## kidsge6, family = binomial, data = mroz)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1765 -0.9177 0.4561 0.8635 2.1897
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.655229 0.848897 0.772 0.44020
## educ 0.183817 0.040353 4.555 5.23e-06 ***
## exper 0.209716 0.031970 6.560 5.39e-11 ***
## I(exper^2) -0.003067 0.001010 -3.035 0.00241 **
## age -0.093873 0.014352 -6.541 6.13e-11 ***
## kidslt6 -1.424937 0.201669 -7.066 1.60e-12 ***
## kidsge6 0.049493 0.074132 0.668 0.50437
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1029.75 on 752 degrees of freedom
## Residual deviance: 810.21 on 746 degrees of freedom
## AIC: 824.21
##
## Number of Fisher Scoring iterations: 4It is highly important to note that because our independent variables are related to the dependent variables through a linking function, we cannot simply interpret the coefficients in the above model. We can still interpret the sign and significance
Like our linear models, we can use the AIC, BIC, and stepwise-regression tools with the same commands:
AIC(model2)## [1] 824.2056BIC(model2)## [1] 856.574step(model2)## Start: AIC=824.21
## inlf ~ educ + exper + I(exper^2) + age + kidslt6 + kidsge6
##
## Df Deviance AIC
## - kidsge6 1 810.65 822.65
## <none> 810.21 824.21
## - I(exper^2) 1 818.51 830.51
## - educ 1 832.30 844.30
## - exper 1 851.53 863.53
## - age 1 857.74 869.74
## - kidslt6 1 869.10 881.10
##
## Step: AIC=822.65
## inlf ~ educ + exper + I(exper^2) + age + kidslt6
##
## Df Deviance AIC
## <none> 810.65 822.65
## - I(exper^2) 1 818.94 828.94
## - educ 1 832.37 842.37
## - exper 1 851.59 861.59
## - age 1 868.88 878.88
## - kidslt6 1 872.08 882.08##
## Call: glm(formula = inlf ~ educ + exper + I(exper^2) + age + kidslt6,
## family = binomial, data = mroz)
##
## Coefficients:
## (Intercept) educ exper I(exper^2) age
## 0.918083 0.181449 0.207825 -0.003058 -0.097216
## kidslt6
## -1.446093
##
## Degrees of Freedom: 752 Total (i.e. Null); 747 Residual
## Null Deviance: 1030
## Residual Deviance: 810.7 AIC: 822.7The white correction for heteroskedasticity also works in this case.
The broom package will also work with GLM models, although it gives different summary statistics in the glance because things like the R-squared have different definitions for logistic models:
glance(model2)## # A tibble: 1 x 7
## null.deviance df.null logLik AIC BIC deviance df.residual
## <dbl> <int> <dbl> <dbl> <dbl> <dbl> <int>
## 1 1030. 752 -405. 824. 857. 810. 746mcfaddenR2 <- 1-glance(model2)$deviance/glance(model2)$null.deviance
mcfaddenR2## [1] 0.2131989The McFadden’s R-squared is a simple statistic that is commonly used to evaluate logistic models.
As before we can plot our logistic models. Notice that the logistic curve is fixed to being between 0 and 1 whereas the linear probability model can predict values outside of that range:
ggplot(mroz,aes(x=exper,y=inlf)) + geom_point() +
geom_line(aes(y=predict(lm(inlf~exper,data=mroz))),color="red",size=2)+
geom_line(aes(y=predict(glm(inlf~exper,family=binomial(),data=mroz),type="response")),color="blue",size=2) +
scale_x_continuous('Experience (years)') +
scale_y_continuous('In the labor force (binary)')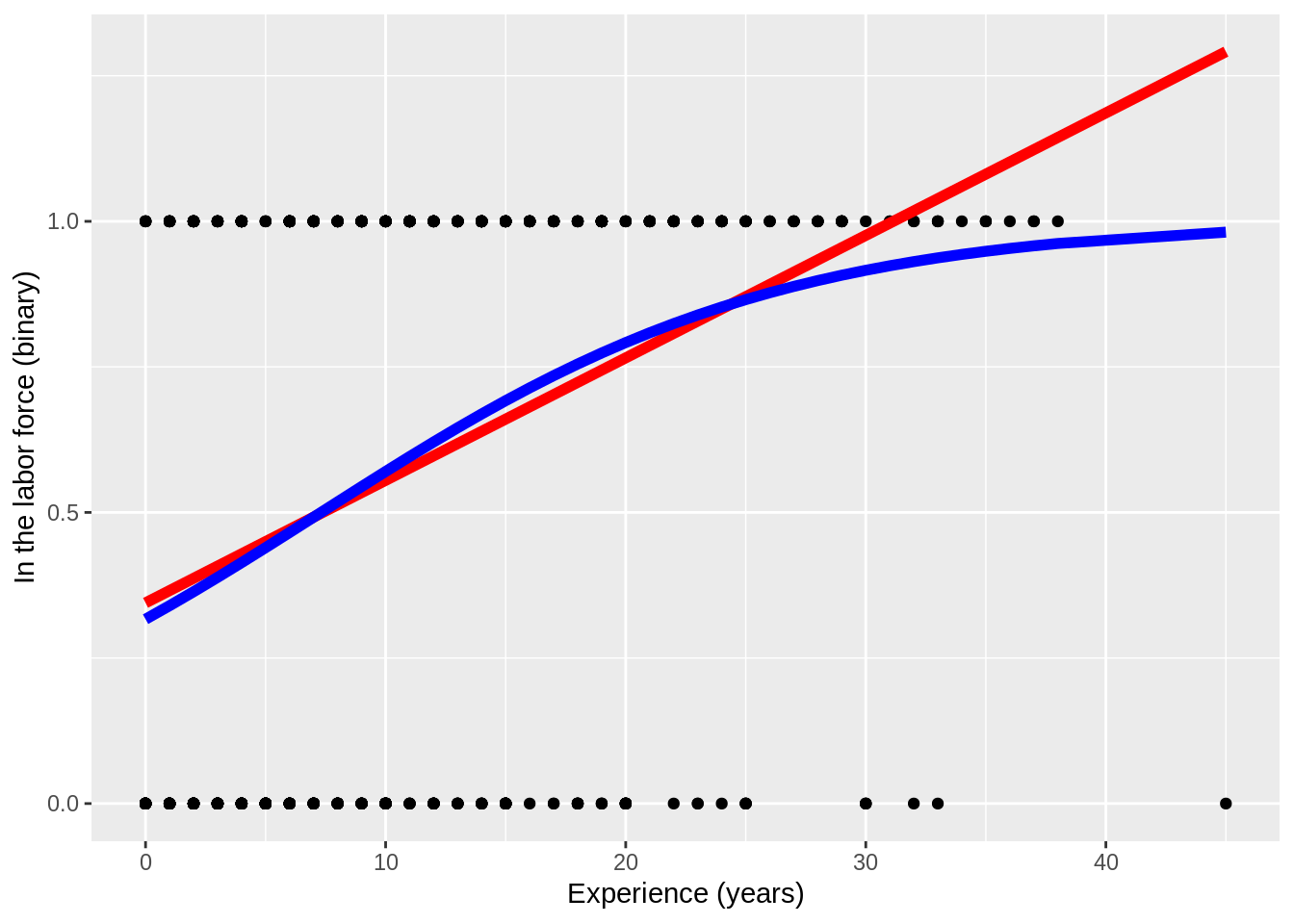
4.2.3 Margins and prediction
Predictions can be performed for logistic models using the predict function, however, it is important to note that without setting type="response" the logistic model will give prediction without applying the linking function (scaled between \(-\infty\) and \(\infty\)):
predict(model2,newwomen)## 1 2 3
## 1.752014 3.131332 -3.812244predict(model2,newwomen,type="response")## 1 2 3
## 0.85220661 0.95816683 0.02162074To find out how a given change in the independent variables affects the dependent variables, we can use the margins package:
library(margins)
margins(model2)## Average marginal effects## glm(formula = inlf ~ educ + exper + I(exper^2) + age + kidslt6 + kidsge6, family = binomial, data = mroz)## educ exper age kidslt6 kidsge6
## 0.03315 0.02669 -0.01693 -0.2569 0.008925Here we can see that a 1 year increase in education relates to a 3.3% increase in the probablity of being in the labor force on average. We can also see that having a child less than 6 years old relates to a 25.7% decrease in the probability of being in the labor force on average. These effects are the average marginal effect. The marginal effect for a particular woman may vary, but this is the average across the data that we have.
4.2.4 Probit regression
Similar to the logit model, we can run probit regression using the glm function. Unlike the logit, we now have to specify the linking function which we set to probit in this case:
model3 <- glm(inlf~educ+exper+I(exper^2)+age+kidslt6+kidsge6,
family=binomial(link="probit"),data=mroz)
summary(model3)##
## Call:
## glm(formula = inlf ~ educ + exper + I(exper^2) + age + kidslt6 +
## kidsge6, family = binomial(link = "probit"), data = mroz)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2179 -0.9291 0.4367 0.8694 2.2242
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.4007652 0.5026692 0.797 0.42529
## educ 0.1098671 0.0236744 4.641 3.47e-06 ***
## exper 0.1259599 0.0187190 6.729 1.71e-11 ***
## I(exper^2) -0.0018430 0.0005977 -3.083 0.00205 **
## age -0.0562898 0.0083325 -6.755 1.42e-11 ***
## kidslt6 -0.8597332 0.1172406 -7.333 2.25e-13 ***
## kidsge6 0.0305577 0.0437973 0.698 0.48536
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1029.75 on 752 degrees of freedom
## Residual deviance: 808.89 on 746 degrees of freedom
## AIC: 822.89
##
## Number of Fisher Scoring iterations: 4The rest of the modeling can be done in exactly the same way as the logit. Statically, both methods are valid for the same use cases. Typically we want to use logit because it’s both simpler to compute and it has a longer history in practice.
4.2.5 Poisson regression and others
Another simple GLM is poisson regression for count data. Here we are considering the crime1 dataset which looked at people recently paroled out of prison in the US and their number of arrests in their first year outside. We model the number of arrests using the total time they spend in prison, their quarters of employment in their year outside, their income in that year, and some dummy variables for race. Obviously we can simply run the linear model:
model4 <- lm(narr86~tottime+qemp86+inc86+black+hispan,data=crime1)
summary(model4)##
## Call:
## lm(formula = narr86 ~ tottime + qemp86 + inc86 + black + hispan,
## data = crime1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.8130 -0.4774 -0.2630 0.3000 11.5627
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.4826032 0.0321423 15.015 < 2e-16 ***
## tottime -0.0007269 0.0035128 -0.207 0.83609
## qemp86 -0.0370450 0.0141983 -2.609 0.00913 **
## inc86 -0.0015502 0.0003420 -4.533 6.07e-06 ***
## black 0.3303553 0.0455112 7.259 5.07e-13 ***
## hispan 0.1835112 0.0398553 4.604 4.33e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8334 on 2719 degrees of freedom
## Multiple R-squared: 0.06058, Adjusted R-squared: 0.05885
## F-statistic: 35.07 on 5 and 2719 DF, p-value: < 2.2e-16Here we see that having 1 extra quarter of employment is related to having 0.037 fewer arrests in the year ’86. This kind of interpretation doesn’t make sense for most of our data (people who were arrested 0 times). It’s also difficult to internalize. What does 0.037 fewer arrests really mean to the average person in this data set? Instead, we would like to interpret a percentage effect from quarters of employment. We would normally do this by taking the log of the dependent variable however, this is impossible here because the dependent variable is number of arrests and most of our data has 0 arrests and it’s impossible to take the log of zero. Instead we are going to use poisson regression for this task.
To run a poisson regression use the GLM with the family set to poisson. The linking function will default to the natural log, so we can interpret the following model just as we would interpret a model where the y variable has been logged.
model5 <- glm(narr86~qemp86+black+hispan,family=poisson,data=crime1)
summary(model5)##
## Call:
## glm(formula = narr86 ~ qemp86 + black + hispan, family = poisson,
## data = crime1)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.3674 -0.9105 -0.7107 0.2691 7.7354
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.77732 0.05723 -13.582 < 2e-16 ***
## qemp86 -0.19962 0.01892 -10.549 < 2e-16 ***
## black 0.70994 0.07355 9.653 < 2e-16 ***
## hispan 0.49557 0.07360 6.733 1.66e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 3208.5 on 2724 degrees of freedom
## Residual deviance: 2957.3 on 2721 degrees of freedom
## AIC: 4640.6
##
## Number of Fisher Scoring iterations: 6Here, every 1 quarter of employment is related to having a 20.0% decrease in the number of arrests in ’86 on average.